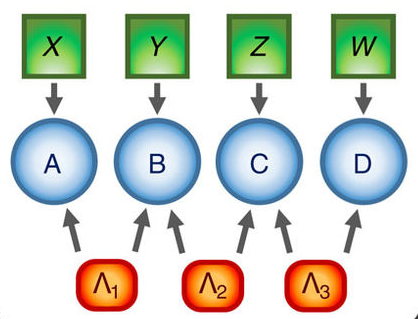
We investigate generalizations of Bell's theorem to a broad variety of relevant scenarios, also trying to understand how to use these non-classical correlations as physical resource in device-independent applications ranging from universal quantum computation to quantum cryptography, randomness generation and efficient distributed computing over complex networks.

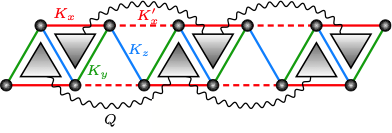
We use a combination of exactly solvable models, low-energy effective field theories and numerical methods to investigate quantum phases of matter and unconventional phase transitions. For instance, the continuous transition between a chiral spin state and collinear magnetic state in a zigzag chain with multi-spin interactions has analogies with deconfined quantum criticality in higher dimensions.

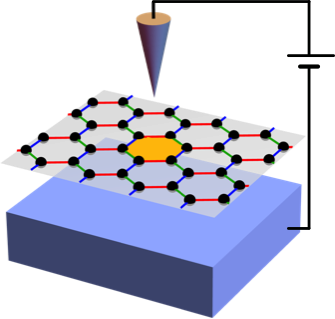
Quantum spin liquid phases in frustrated magnets can harbor fractional quasiparticles with exotic properties that may be useful for topological quantum computation. We have proposed new ways to detect and manipulate Majorana zero modes using electric fields and scanning tunneling spectroscopy in Kitaev materials.

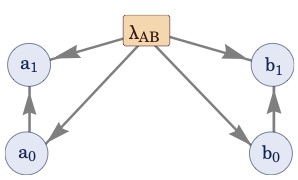
We develop the conceptual and mathematical tools to understand the role of causality in quantum mechanics. From a fundamental perspective, our aim is to identify which causal structures yield quantum correlations without a classical analogue. From the practical side, we are interested in developing new applications, from experimentally less demanding cryptographic protocols to more efficient ways to communicate within complex quantum networks.